颗粒填充问题研究颗粒形状、粒径分布以及局部填充结构对填充体几何和物理特性的影响。自1611年开普勒猜想提出以来,颗粒填充问题一直是数学和物理学领域的重要课题,同时在科学研究和工程领域也有着广泛的应用,如液体结构、纳米颗粒自组装、液晶、玻璃态和生物材料等。颗粒形状对颗粒填充的结构和特性有着决定性的影响,不同形状的颗粒在致密化过程中会表现出多种多样的液相、塑晶和晶体结构。四面体是最简单的柏拉图实体,由于缺乏反对称性使其在填充中呈现出十分独特的性质,因此受到广泛关注。正四面体的最密填充也是希尔伯特第18问题的一部分,目前得到的正四面体最高填充率为4000/4671(约为0.8563)。然而值得注意的是,实际四面体颗粒的边缘均有不同程度的圆角。
最近,williamhill体育在线登录李水乡">李水乡课题组对理想正四面体颗粒引入圆角变化的形状参数,研究了颗粒形状从理想正四面体连续变化到球体的密填充结构。整个演化过程呈现出了不同的密填充结构,大致可以分为变形的二聚晶体结构、变形的准晶近似体、变形的六方密堆积和变形的面心立方堆积结构。根据结构单元变化的不连续性,又可以将这些构型细分为八个分区。该研究结果有助于进一步理解球体到非球体的形状变化对填充性质的影响,并佐证了Ulam猜想,即球体是所有凸体中填充率最低的形状。此外,在圆角度增大过程中,出现了填充率先增加后下降的特殊变化趋势。带有小圆角的球四面体(圆角度s=0.16)的填充率可达0.8763,超过了目前已知的理想正四面体最高填充率。
相关研究成果近期在Nature旗下期刊Scientific Reports在线发表(www.nature.com/articles/srep15640),论文题目为“Evolution of the dense packings of spherotetrahedral particles: from ideal tetrahedra to spheres”。论文第一作者为博士研究生金炜炜。该项研究得到了国家重点基础研究发展计划和国家自然科学基金的支持。
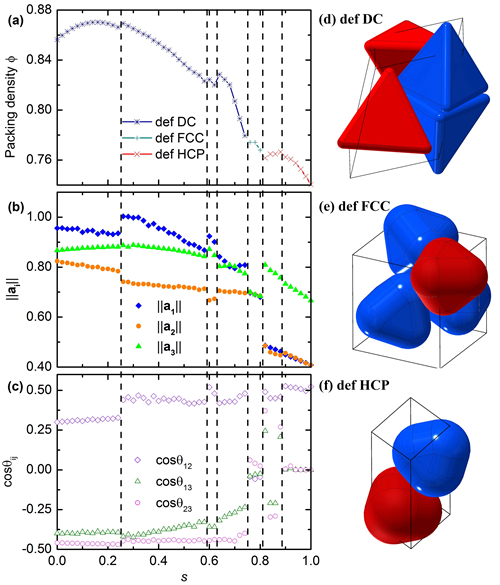
密填充率(a)和结构单元参数(b)(c)随圆角度s的变化以及三种典型的填充结构单元:变形的二聚晶体结构(d),变形的面心立方堆积结构(e)和变形的六方密堆积结构(f)










